写在前面

机器学习是以算法为核心，理解算法也为了帮助我们更好的理解程序。举个栗子：写程序就像开一辆车，当你不懂太多数据结构跟算法的时候，凭借丰富的实践经验你也可以将这辆车开好；但是，当有一天这辆车出问题跑不起来的时候呢？你不懂它内部的运行机制，你要怎么排除和解决问题？

欢迎关注公众号：AI数据分析算法

主要内容

简单介绍

逻辑回归（也称“对数几率回归”）（英语：Logistic regression 或logit regression），即逻辑模型（英语：Logit model，也译作“评定模型”、“分类评定模型”）是离散选择法模型之一，属于多重变量分析范畴，是社会学、生物统计学、临床、数量心理学、计量经济学、市场营销等统计实证分析的常用方法。

—–维基百科

逻辑回归的一般过程：

收集数据
准备数据：由于需要进行距离计算，所以要求数据类型为数值型
分析数据
训练算法：为了找到最佳的分类回归系数，即寻找最佳拟合参数
测试算法

优点：计算代价不高，易于理解和实现

缺点：容易过拟合，分类精度可能不高

适用数据类型：数值型和标称型数据

以上内容参考于《机器学习实战》一书

标称型数据：标称型目标变量的结果只在有限目标集中取值，如真与假(标称型目标变量主要用于分类)

算法推导

最大似然估计

在进行Logistic Regression 算法推导前，让我们先来了解一下贝叶斯决策和最大似然估计。
$$
P(w|x) = \frac{P(x|w)\cdot P(w)}{P(x)}
$$
$P(w|x)$为后验概率，$P(x|w)$为类条件概率，$P(w)$为先验概率，而$P(x)$为全概率。

如果对贝叶斯公式还是不太了解的，希望能够去了解贝叶斯公式，最好是做一道题目，这里就不详细讲述。

但是在实际问题中我们能获得的数据可能是有限数目的数据，而先验概率和类条件(各类的总体分布)都是未知的。所以我们仅能根据有限的样本集进行分类。有一种可行的办法就是我们需要先对先验概率和类条件概率进行估计，然后再运用贝叶斯分类器。

先验概率的估计比较简单：每个样本所属的I自然状态都是已知的，依靠经验，或者是用训练样本中各类出现的频率估计。

然后类条件概率的估计是非常困难的，概率密度函数包含了一个随机变量的全部信息，样本数据可能不多，再者特征向量的维度可能很大。所以解决办法，是把估计完全未知的概率密度转化为估计参数。极大似然估计就是一种参数估计方法。

举个例子，有两个箱子，分别都有100个球，左边的箱子有99个白球和1个黑球；右边的箱子是有99个黑球和1个白球，试着取出一个球，结果是黑球。试问，黑球是从哪个箱子中取出来的。
分析：当我们考虑这个问题，大部分都会猜黑球最有可能从右边的箱子里面取出来的。因为概率非常大，这也是符合我们正常的认知。而这种认知，“最像”,“最有可能”其实就是“最大似然”的意思，这种想法也常常称为“最大似然原理”。

目的就是：利用已知的样本结果，反推最有可能导致这样结果的参数。
实验原理：模型已定，参数未知，我们需要通过若干次实验，观察结果，利用实验结果得到某个参数值能够使样本出现的概率最大，则称为“极大似然估计”。

似然函数(likelihood function)：联合概率密度函数$P(D|\theta)$称为相对于$D={x_1,x_2\dots,x_N}$的$\theta$的似然函数。
$$
l(\theta)=P(D|\theta)=P(x_1,x_2,\dots,x_N|\theta) = \prod_{i=1}^NP(x_i|\theta)
$$
如果$\hat\theta$是参数空间中能使似然函数最大的值，则该$\hat\theta$就是$\theta$的极大似然估计量。而$\hat{\theta}(x_1,x_2,\dots,x_N)$称作极大似然函数的估计值。

求解极大似然估计

$$
\hat{\theta}={argmax}h(\theta) = argmaxln(\theta) = argmax\sum_{i=1}^NlnP(x_i|\theta)
$$

构造预测函数

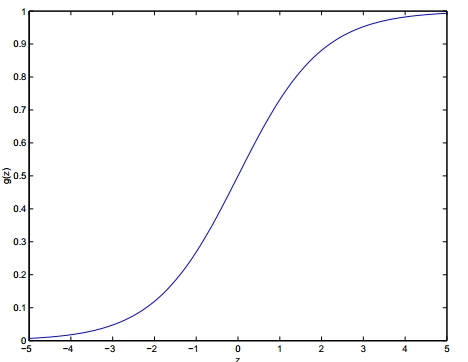
我们需要找到一个预测函数$h_\theta$，显然该函数的输出必须有两个值，分别代表两个类别。所以我们使用了Sigmoid函数，以下为公式：
$$
g(z) = \frac{1}{1+e^{-z}}
$$
下面是该函数的图像。

根据NG所讲的机器学习中，接下来需要确定数据划分的边界类型，下面我们讨论线性边界的情况。

对于线性边界的情况，有以下形式：
$$
\theta_0+\theta_1x_1+\dots+\theta_nx_n = \sum_{i=0}^n\theta_ix_i = \theta^Tx
$$
构造预测函数：
$$
h_\theta(x) = g(\theta^Tx) = \frac{1}{1+e^{-\theta^Tx}}
$$
因此对于输入x分类结果为类别1和类别0的概率分别为：
$$
\begin{align}
&P(y=1|x;\theta) = h_\theta(x) \\
&P(y=0|x;\theta) = 1-h_\theta(x)
\end{align}
$$

构造Cost函数(代价函数)

将上述的方程组综合：
$$
P(y|x;\theta)=(h_\theta(x)^y)((1-h_\theta(x))^{1-y})
$$
通过似然函数变为：
$$
L(\theta) = \prod_{i=1}^mP(y^{(i)}|x^{(i)};\theta)
$$
$i$为样本数为，共有m个样本。

然后对$L(\theta)$取负对数，可得：
$$
\begin{align}
l(\theta) & = -logL(\theta)\\
& = -\sum_{i=1}^m(y^{(i)}logh_\theta(x^{(i)})+(1-y^{(i)})log(1-h_\theta(x^{(i)})))
\end{align}
$$
令$J(\theta)=cos(h_\theta(x);y)$构造代价函数：
$$
J(\theta)= -\frac{1}{m}\sum_{i=1}^m(y^{(i)}logh_\theta(x^{(i)})+(1-y^{(i)})log(1-h_\theta(x^{(i)})))
$$
所以需要求解$\hat{\theta}$为最佳参数，所以只要求$J(\theta)$的最小值

梯度下降法求解$J(\theta)$的最小值

根据梯度下降法可得$\theta$的更新过程：
$$
\theta_j := \theta_j - \alpha\frac{\partial}{\partial\theta_j}J(\theta) \qquad (j = 0,1,2,\dots n)
$$
$\alpha$为学习的步长，下面来求步长，对$\theta$求偏导：

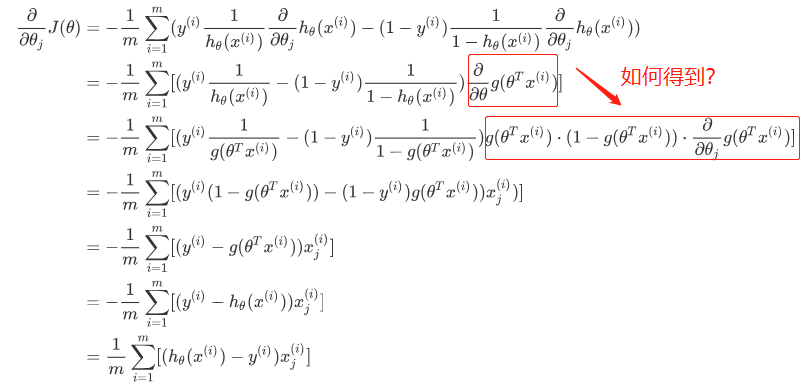
所有更新：
$$
\theta_j : = \theta_j - \alpha\sum_{i=1}^{m}[(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)}]
$$

这里写一下红色框框的步骤：

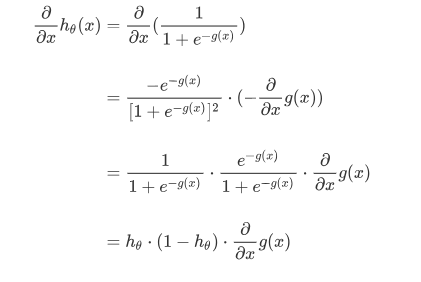
向量化梯度下降

可观察上面的更新过程，是有求和符号$\sum$，所以并没有向量化，下面我们通过矩阵的方式对梯度下降进行推导。
$$
X = \begin{bmatrix} x^{(1)} \\ x^{(2)} \\ \vdots \\ x^{(m)}\end{bmatrix} = \begin{bmatrix} x_0^{(1)} & x_1^{(1)} &x_2^{(1)}& \cdots x_n^{(1)} \\ \vdots &&&\vdots \\ \vdots&&&\vdots\\ x_0^{(m)}&\cdots&\cdots&x_n^{(m)}\end{bmatrix}
$$
从上面可以看出，这是一个$m\times(n+1)$的矩阵，定义有m个样本，和(n+1)个特征。

待求参数$\theta$(权重：weights)的矩阵为：
$$
\Theta =
\begin{bmatrix}
\theta_0\\
\theta_1\\
\vdots\\
\theta_n
\end{bmatrix}
$$

求$X\cdot\Theta$记作A：
$$
A = \begin{bmatrix} x_0^{(1)} & x_1^{(1)} &x_2^{(1)}& \cdots x_n^{(1)} \\ \vdots &&&\vdots \\ \vdots&&&\vdots\\ x_0^{(m)}&\cdots&\cdots&x_n^{(m)}\end{bmatrix} \cdot \begin{bmatrix}
\theta_0\\
\vdots\\
\vdots\\
\theta_n
\end{bmatrix} = \begin{bmatrix} x_0^{(1)}\theta_0+x_1^{(1)}\theta_1+\cdots+x_n{(1)}\theta_n \\
x_0^{(2)}\theta_0+x_1^{(2)}\theta_1+\cdots+x_n{(2)}\theta_n \\
\vdots \\
\vdots \\
x_0^{(m)}\theta_0+x_1^{(m)}\theta_1+\cdots+x_n{(m)}\theta_n
\end{bmatrix}
$$
标签y为：
$$
Y =
\begin{bmatrix}
y^{(1)}\\
y^{(2)}\\
\vdots\\
y^{(n)}
\end{bmatrix}
$$

设$E= h_\theta(\theta\cdot X) - Y$，即可计算得：
$$
E =
\begin{bmatrix}
g(A^{(1)})-y(1) \\
\vdots\\
\vdots\\
g(A^{(m)})-y^{(m)}
\end{bmatrix}= \begin{bmatrix}
e^{(1)}\\
e^{(2)}\\
\vdots\\
e^{(m)}
\end{bmatrix}= g(A) - Y
$$

当$j=0$时候，只有一个特征的时候，可得：

$$
\begin{align} \theta_0:
& = \theta_0 - \alpha \sum_{i=1}^m[h_\theta(x^{(i)})-y(i)]x_0^{(i)} \\
& = \theta_0 - \alpha\sum_{i=1}^me^{(i)}\cdot x_0^{(i)}\\
& = \theta_0 - \alpha(x_0^{(1)}, x_0^{(2)},\dots,x_0^{(m)})\cdot E
\end{align}
$$

进而可以推断出当$j = n$的时候的情况：

$$
\theta_j : \theta_j = \alpha(x_j^{(1)}, x_j^{(2)},\dots,x_j^{(m)})
$$

最后可以写成：
$$
\begin{bmatrix}
\theta_0\\
\theta_1\\
\vdots\\
\theta_n
\end{bmatrix}= \begin{bmatrix}
\theta_0\\
\theta_1\\
\vdots\\
\theta_n
\end{bmatrix}- \alpha\cdot\begin{bmatrix}
x_0^{(1)} & x_0^{(2)} &x_0^{(3)}& \cdots x_0^{(m)} \\
x_1^{(1)} & x_1^{(2)}& \cdots&\vdots \\
\vdots&&&\vdots\\
x_n^{(1)}&\cdots&\cdots&x_n^{(m)}
\end{bmatrix} \cdot E
$$

可以简写成：
$$
\begin{align}
&= \Theta - \alpha \cdot X^T \cdot E \\
&= \Theta - \alpha\cdot X^T \cdot(g(\theta^TX)-Y)
\end{align}
$$

总结

Logistic 回归的目的就是寻找一个非线性函数Sigmoid的最佳拟合参数，求解过程可以由最优化算法来完成。

以上就是Logistic Regression的算法总结，如有错误，希望指出。

打个广告，欢迎关注自家公众号：AI数据分析算法

有更多的分享资料和交流小伙伴。