写在前面
本文是并不是完全对于CS231n课程的全部翻译,只是作者对课程的一个总结的笔记记录。如有错误的地方,请指出并留言,作者十分感谢。如果想查看原版笔记,可以查看下面CS231n-notes,点击则可查看。
关注公众号:AI数据算法分析
大家一起进步学习人工智能。
主要内容
此篇内容主要讲CS231n课程内容,根据B站课程内容P4部分的笔记总结。
- 图像分类、数据驱动方法和流程
- Nearest Neighbor分类器
图像分类
课程开始于5:09左右,如果大家想直接进入课程的,可以直接跳到5分09秒开始。

如上图,图片分类是计算机视觉的核心任务。
目标:所谓图像分类,就是将已经做好了标签的图片进行分类,将一个个图片元素分为一个个集合。然后对于输入的图像,从分类标签集合中找出一个分类标签,最后把分类标签分配给该输入图像。
例子:如上图,计算机通过对图像进行分类,并生成集合,比如{cat,dog,pig,plane,..},然后对输入的图像进行计算,得到在集合中标签的的概率,从而来预测图片属于哪个分类。
计算机中的图片:
计算机是如何识别图片的,当然是和我们识别图片的方法不一样。图像是由一个巨大的三维数组组成的,在上述图片的例子中。这张图片的分辨率是248$\times$400,就可以说这张图片的长度是248个像素,高有400个像素;并且这是一张彩色图片,因此有3个颜色通道,分别是红绿蓝,简称RGB。所以该图像总共有$248\times400\times3=297600$个数字。由于RGB三个三原色的强度范围都是0~255,其中0表示全黑,255就表示全白。
我们的目标和任务就是把这些上百万的数字变成一个简单的标签,用来预测输入的图片。如下图所示。
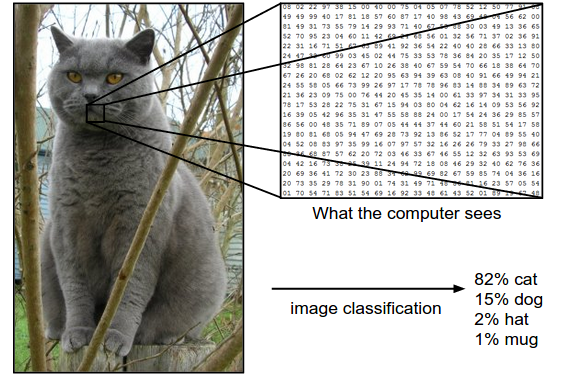
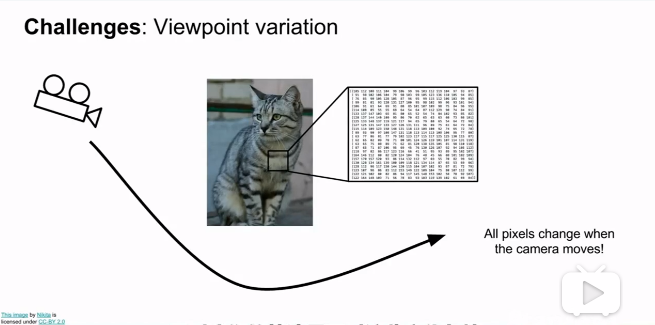
虽然是对于图片的简单的分类,对于我们来说,识别一只猫是非常简单的。但是对于计算机来说,还是有一定的困难,会遇到一定的问题。
下面列举了可能遇到的问题,取自于课程的内容。
视觉变化(Viewpoint variation):同一个物体,摄像机可以从多个角度来展现。

大小变化(Scale variation):物体可视的大小通常是会变化的。

形变(Deformation):很多东西的形状并非一成不变的,会有很大的变化

遮挡(Occlusion):目标物体有可能被一些杂物遮挡,有时候只有物体的一小部分,甚至就单单的几个像素点

光照条件(Illumination condition):在像素层面上,光照的影响非常大

背景干扰(Background clutter):物体可能混入背景之中,使其物体难以被辨认

类内差异(Intra-class variation):一类物体的个体之间的外形差异很大,比如飞机,有客机,战斗机,隐形飞机,直升机等,都有自己的特征。

数据驱动方法
数据驱动,其实就是给计算机很多数据,不停的“喂”食物。然后实现学习算法,让计算机学习到每个类的特征。
数据驱动方法的步骤:
- 收集图片以及标签的数据集,也称此数据集为训练集(train set)
- 使用机器学习来训练一个分类器
- 通过分类器来评估预测一张新的图片,把分类器预测的标签和图像真正的分类标签作对比
我们来看一看收集的数据集,如下图所示,只有4个分类的训练集。但在实际中,我们可能有上千分类,每个分类都有成千上万的图像。

Nearest Neighbor 分类器
作为课程的介绍的第一个方法,来实现图片分类。但是实际上用的比较少,甚至说极少,但对于新手来说,可以对解决图像分类方法有个初步的认识。
举例:
图像分类数据集:CIFAR10
这个数据集有10个分类,50000个训练集图片以及10000张测试集图片。左边是样本图像。右边的第一列是测试图像,箭头右边的则是使用Nearest-Neighbor算法,从训练集中选出最类似的10张图片。
可以观察出,例如第一行,飞机被分错了,可有可能的原因就是,背景颜色都是黑的,这才导致被判断错误。可以看出虽然图片分类的准确度没有那么高,但这仍然是一个好的demo。那具体是如何比较两张图片呢?是如何进行分类的呢?
这里用的到方式是逐个像素的比较,最后将他们的差异值全部加起来。换句话说,就是将图片转化为两个向量$I_1$和$I_2$,然后计算他们的$L_1$距离(曼哈顿距离)。
$$
d_1(I_1,I_2)=\sum_p|I_1^p-I_2^p|
$$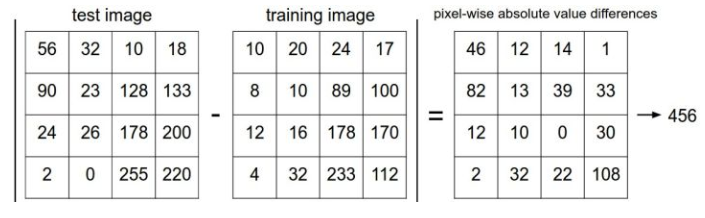
差异值越小,说明图片就越相似。
下面,我们来通过代码实现这个分类器。首先,将数据集加载到内存中,并分为4组。分别是训练特征(Xtr)、训练标签(Ytr)、测试特征(Xte)、测试标签(Yte)。Xtr的大小是$50000\times32\times32\times3$,而Ytr则是一个$50000\times1$,每个数值大小的范围是0~9(因为一共有10个分类)。
1 | Xtr, Ytr, Xte, Yte =load_CIFAR10('data/cifar10') #loaddown all of images |
下面是L1距离的Nearest Neighbor分类器的实现:
1 | import numpy as np |
用这个方法的准确率远不如CNN(卷积神经网络),所以也是极少用的原因。
当然距离不止是曼哈顿距离一个,还有欧式距离($L_2$距离),公式如下:
$$
d_2(I_1,I_2)=\sqrt{\sum_p(I_1^p-I^p_2)^2}
$$
代码如下:
1 | distances = np.sqrt(np.sum(np.square(self.Xtr-X[i,;], axis = 1))) |
注意在这里使用了np.sqrt,但是在实际中可能不用。因为求平方根函数是一个单调函数,它对不同距离的绝对值求平方根虽然改变了数值大小,但依然保持了不同距离大小的顺序。所以用不用它,都能够对像素差异的大小进行正确比较。
L1和L2比较。比较这两个度量方式是挺有意思的。在面对两个向量之间的差异时,L2比L1更加不能容忍这些差异。也就是说,相对于1个巨大的差异,L2距离更倾向于接受多个中等程度的差异。
具体可参考:机器学习数学基础(一),里面讲解了具体的P-norm。
K-Nearest Neighbor 分类器
原理:
与其只找最近的那一个图片的标签,不如找相似的K个图片的标签,然后进行投票,票数最多的标签得胜,作为该预测图片的标签。这样就让分类的效果更平滑,对异常值更有抵抗力。
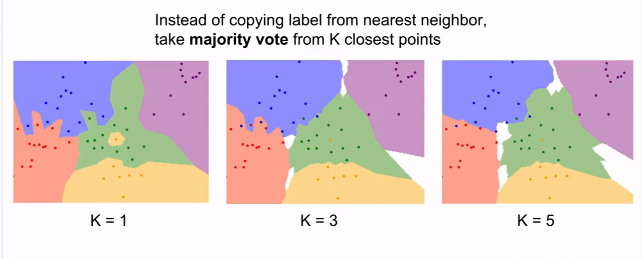
从上面的示例可以看出,不同颜色的区域代表的是使用L1距离的分类器的决策边界。白色区域表示不同类别投票数相同时的预测模糊区域(图像与两个以上的分类标签绑定)。需要注意的就是异常数据点,比如3-NN分类器中,红色区域中有紫色的点,导致在紫色区域内有一个红色凸起预测区域,这也表示出现了过拟合现象,即使是训练数据的噪声也进行了很好地学习。但是在5-NN中,整个区域边界就变得非常的平滑,这说明对测试数据的泛化能力更好。
下一章,就讲解K-NN算法,如何确定K值,请关注CS231n笔记(2)—KNN算法。


