写在前面

这里接精读西瓜书二内容，仍然讲的是模型的评估与选择，主要是性能度量。

知识点归纳

性能度量

先复习一下，机器学习理想的目标。

通过评估学习器的泛化误差，选出泛化误差最小的学习器。

上一节，通过不同的评估方法来选出最终的模型，但是对于学习器的泛化能力进行评估，仅仅评估方法是不够的，还需要有衡量模型泛化能力的评价标准，这就是性能度量(performance measure)。

【性能度量(performance measure)】：衡量模型泛化能力的评价标准

性能度量反映了任务需要，在对比不同模型的能力时，使用不同的性能度量往往会导致不同的评价结果。因此，什么样的学习器是好的，不仅仅取决于算法和数据，还决定于任务需求。

在预测任务中，$y_i$是示例$x_i$的真实标记，要评估学习器$f$的性能，需要把学习器预测结果$f(x)$与真实标记$y$进行比较。

因为有标记，所以讨论的是监督性学习。

回归任务

均方误差

【均方误差(mean squared error)】:回归任务最常用的性能度量。
$$
E(f;D) = \frac{1}{m} \sum_{i=1}^m (f(x_i)-y_i)^2
$$
可知，均方误差是m个离散样本的方差的平均数

但对于数据分布$D$和概率密度函数$p(\cdot)$，均方误差可描述为：
$$
E(f;D)=\int_{x \sim D}(f(x)-y)^2p(x)dx
$$
可以看出，此时样本可以看做非离散样本而是连续样本。

分类任务

错误率与精度

这是分类任务中最常用的两种性能度量，既适用于二分类任务，也适用于多分类任务。

错误率:分类错误的样本占总样本的比例

精度：分类正确的样本总样本的比例

【错误率公式】：
$$
E(f;D)=\frac{1}{m} \sum_{i=1}^m \mathbb{I}(f(x_i)\ne y_i)
$$
其中$$ \mathbb{I} (\cdot)$$为指示函数(indicator function)，真为1，假为0。常用于次数(满足某一断言或条件)的统计

错误率是m个离散样本的指示函数和的平均数

【精度公式】:
$$
\begin{align}
acc(f;D) & =\frac{1}{m}\sum_{i=1}^m \mathbb{I}(f(x_i)=y_i) \
& = 1-E(f;D) \
\end{align}
$$
精度和错误率相同，也是m个离散样本的指示函数和的平均数，但是两个的指示函数不同。

但是，对于数据分布$D$和概率密度函数$p(\cdot)$，错误率与精度可分别描述为：
$$
E(f;D)=\int_{x \sim D}\mathbb{I}(f(x) \neq y)p(x)dx
$$

$$
\begin{align}
acc(f;D) &=\int_{x \sim D}\mathbb{I}(f(x) = y)p(x)dx \
& = 1-E(f;D)
\end{align}
$$

可了解到，此时的样本可以看做费离散样本，也就是连续样本。

性能度量方法：

通常，错误率低、精度高的模型性能好；反之模型性能差。错误率与精度反应的是分类任务模型判断正确与否的能力。

查准率、查全率与F1

错误率和精准率虽然常用，但不能满足所有的需求。当任务需求不是要判断有样本被判别正确与否的时候，而是关注正例以及反例的查出的准确率时，就需要使用其他的性能度量。

在二分类问题中，可根据其真实类别与学习器预测类别的组合划分为真正例(true positive)、假正例(false positive)、真反例(true negative)、假反例(false negative)，分别简称TP、FP、TN、FN，样例总数 = TP + FP + TN + FN。分类结果的“混淆矩阵(confusion matrix)”。

举例：

好西瓜判断成好西瓜，判断正确①【TP】；好西瓜判断成坏西瓜，判断错误②【TN】

坏西瓜判断成好西瓜，判断错误③【FP】；坏西瓜判断成坏西瓜，判断正确④【FN】

其中，①和④都是判断正确，②和③都是判断错误。错误率和精度是①和④、②和③的综合判断，只有判断正确与否的概念，但是没有正例与反例的区别，所以引入查准率【precision】与查全率【recall】。

【查准率】：【真正例样本数】与【预测结果是正例的样本数】的比值

【查全率】：【真正例样本数】与【真实情况是正例的样本数】的比值

查准率是挑出的好瓜里面，有多少是真的好瓜。如果希望选出的瓜中好瓜比例高的话，则可只挑选最有把握的瓜，但这样会难免会漏掉不少好瓜，查准率高了但查全率就会降低。

查全率是挑出来的真的好瓜，占总共好瓜个数的多少。希望将好瓜极可能多地挑出来，则可通过增加选瓜的数量来实现，如果所有西瓜都选上，那么所有的好瓜也必然都被选上，这样查准率就会降低。

一般来说，查准率高时，查全率偏低；查全率高，查准率偏低。通过只在一些简单任务中，查准率和查全率都偏高。

性能度量的方法：1.直接观察数值；2.建立P-R曲线

下面讲P-R曲线图，即以查准率为纵轴，查全率为横轴作图，就可以得到查准率-查全率曲线，简称“P-R曲线”。

值得注意的是，同一个模型，在同一个正例判断标准下，得到的查准率和查全率只有一个，也就是说，在图中应该是只有一个点，而不是一条曲线。

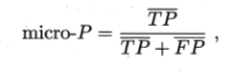
P-R图直观地显示出学习器在样本总体上的查全率、查准率。

可是如何来比较以及判断哪个学习器更优呢？

当没有曲线交叉曲线的时候：外侧学习器性能优于内侧学习器，比如学习器B是优于学习器C

当曲线有交叉的时候：

方法一：比较P-R曲线下的面积大小，但是这个值不太容易估算。

方法二：设计了一些综合考虑查准率、查全率的性能度量。平衡点(Break-Even Point，简称BEP)就是这样一个度量，它是“查准率=查全率”时的取值。基于平衡点的比较，平衡点在外侧的曲线优于内测的，比如学习器A是优于学习器B

方法三：比较常用的是F1度量，F1的来能给的一般形式是$F_\beta$
$$
F1 = \frac{2\times P \times R}{P+R} = \frac{2 \times TP}{样例总数+TP-TN}
$$

F1是基于查准率与查全率的调和平均(harmonic mean)定义的：
$$
\frac{1}{F1}=\frac{1}{2} \cdot (\frac{1}{P}+\frac{1}{R})
$$
$F_\beta$则是加权调和平均：
$$
\frac{1}{F_\beta}=\frac{1}{1+\beta^2} \cdot (\frac{1}{P}+\frac{\beta^2}{R})
$$
调和平均更重视较小值。其中$\beta > 0$度量了查全率对查准率的相对重要性。$\beta = 1$为标准的F1，若大于1，查全率有更大影响；小于1，查准率有更大影响。

以上是一个二分类混淆矩阵的查全率和查准率的判断。

但实际情况中，有多个二分类混淆矩阵。当需要考虑估计算法的全局性能时，希望在N个二分类混淆集镇上综合考察查准率和查全率。有两种方法来解决。

方法1：“宏”：先在各混淆矩阵上分别计算出查准率和查全率，再计算平均值，得到宏查准率(macro-P)、宏查全率(macro-R)、宏F1(macro-F1)

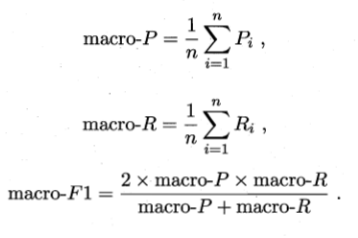
方法2：“微”：先将各混淆矩阵的对应元素进行平均，得到TP、FP、TN、FN的平均值，再基于这些平均值计算出微查准率(micro-P)、微查全(micro-R)率以及微F1(micro-F1)的值。

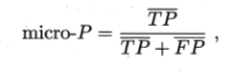
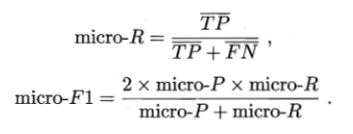
ROC与AUC

ROC曲线图是通过对测试样本设置不同的阈值并与测试值进行比较，划分出正例与反例。再计算出两个重要量的值，分别以它们为横、纵坐标作图，就得到“ROC曲线”。与P-R不同的是，P-R图逐个将样本作为正例，而ROC图是逐次与阈值进行比较后划分正例。ROC曲线的纵轴是“真正例率(True Positive Rate,简称TPR)，横轴是”假正例率”(False Positive Rate，简称”FPR”)。

【真正例率(TPR)】:【真正例样本数】与【真实情况是正例的样本数】的比值（查全率）

【假正例率(FPR)】:【假正例样本数】与【真实情况是反例的样本数】的比值

公式如下：
$$
TPR = \frac{TP}{TP+FN}
$$

$$
FPR=\frac{FP}{TN+FP}
$$

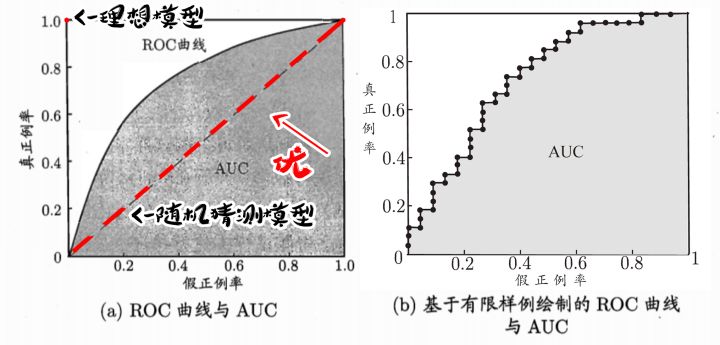
ROC图全名为“受试者工作特征”。

如图，(0,1)点为理想模型。随机模型则是真正例率与假正例率持平的直线，既对角线。

学习器进行比较时，与P-R图相似，若一个学习器的ROC曲线被另一个学习器曲线完全“包住”，则可断言后者的性能优于前者。

若ROC曲线发生交叉，则较为合理的判断是比较ROC曲线下的面积，即AUC(Area Under ROC Curve)。

代价敏感错误率与代价曲线

因为在现实任务中会遇到这样的情况，不同类型的错误所造成的后果不同。拿上面西瓜的例子来说明，如果把好瓜当成坏瓜，等于浪费了一个好瓜；但是把坏瓜当成好瓜，就有可能让顾客吃坏肚子，不得不去就医。因此，为权衡不同类型错误所造成的不同损失，可为错误赋予”非均等代价(unequal cost)。”

说明一点：之前的介绍的性能度量，大多都隐性的假设了”均等假设”。

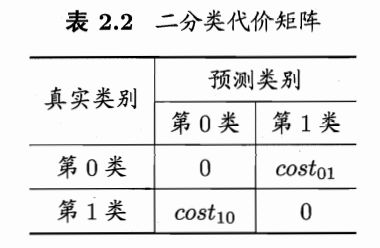
上图为二分类代价矩阵，其中$cost_{ij}$表示将第$i$类样本预测为第$j$类样本的代价。

值得说明一点：一般情况下，重要的是代价比值而非绝对值。例如：$cost_{01} : cost_{10} = 5:1$与$50:1$所起的效果相当。

在非均等代价下，希望做的不再是简单的最小化错误次数，而是希望最小化”总体代价(total cost)”。

例：若将表中第0类作为正例，第1类作为反类，则代价敏感(cost-sensitive)错误率为：
$$
E(f;D;cost)=\frac{1}{m}(\sum_{x_i \in D^+}\mathbb{I}(f(x_i) \neq y_i)\times cost_{01}+ \sum_{x_i \in D^-}\mathbb{I}(f(x_i)\neq y_i)\times cost_{10})
$$
在这样非均等代价下，ROC曲线不能直接反映出学习器的期望总体代价，而“代价曲线(cost curve)”则可以达到该目的。代价曲线图的横轴是取值[0,1]的正例率代价，纵轴是取值[0,1]的归一化代价。
$$
P(+)cost=\frac{p\times cost_{01}}{p\times cost_{01}+(1-p)\times cost_{10}}
$$

$$
cost_{norm} = \frac{FNR\times p\times cost_{01}+FPR\times (1-p)\times cost_{10}}{p\times cost_{01}+(1-p)\times cost_{10}}
$$

其中$p$是样例为正例的概率。

【假反利率(FNR)】：【假反例样本数】与【真实情况是正例的样本数】的比值。(1-查全率)

代价曲线的绘制方法：