写在前面:
函数
- 函数与数据的泛化
- 推理与归纳
线性代数
- 向量与矩阵
- 特征值与特征空间
- 高维空间向量
- 特征向量
函数
定义:
在数学中,函数(function)就是一种关系,是一组输入和一组输出之间的关系,也是映射。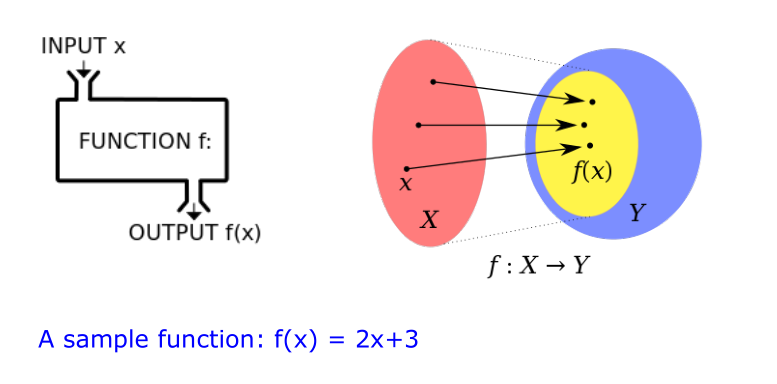
类型
- 1.2.1指数函数(常用作激活函数)
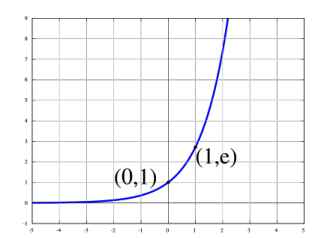
$$
y = e^x
$$
应用链接:动态模型展示链接
- 1.2.2 对数函数(指数函数的反函数)
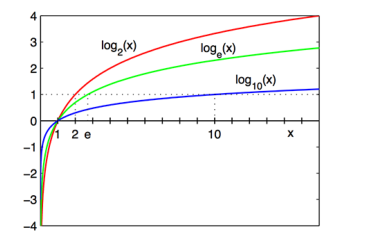
- 1.2.3 sigmoid函数(一般用作激活函数:因为映射到(0,1)之间)
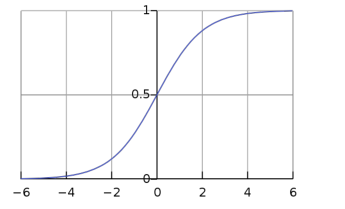
$$
S(x) = \frac{1}{1+e^{-x}} = \frac{e}{e^x+1}
$$
- 线性整流函数(常用的为斜坡函数:rectifier)
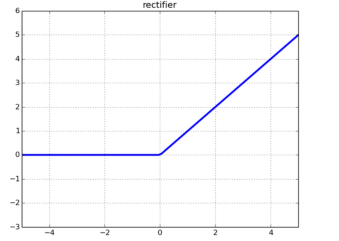
$$
f(x) = max(0,x)
$$
当 x > 0 时,x = y
当 x < 0 时,y = 0
链接:线性整流函数函数
- 复合函数(函数的嵌套,Function Decomposition)
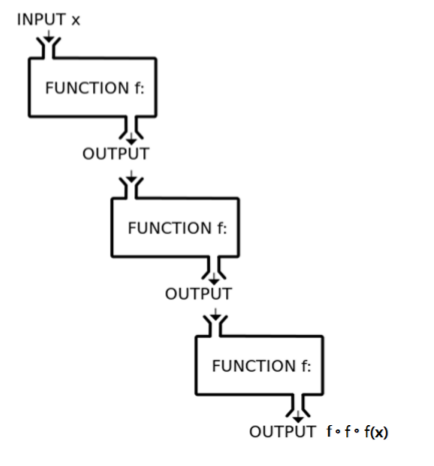
举例:
$$
f(x) = 2x+3
$$
$$
f(f(x)) = 2(2x+3)+3 = 4x + 9
$$
动态函数和静态函数
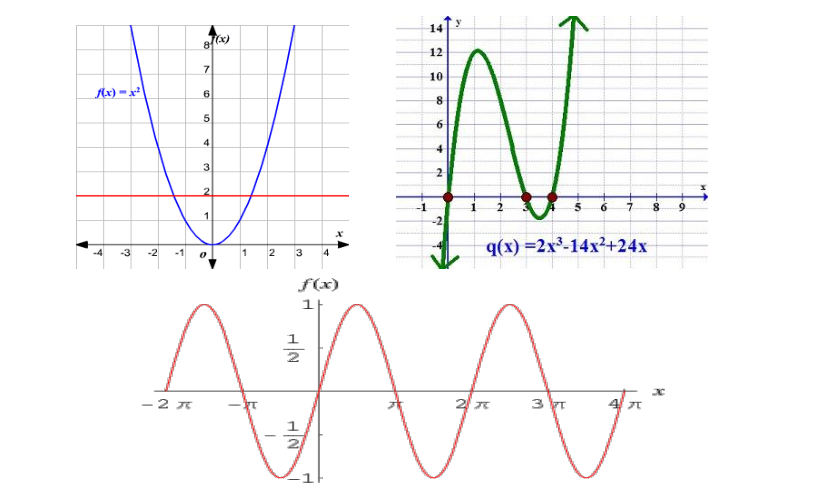
上面为静态函数,下面为动态函数
区别:动态函数的输入是和时间有关系,静态函数的输入则和时间没有关系
比较接近现实的函数(The Real-World Data)
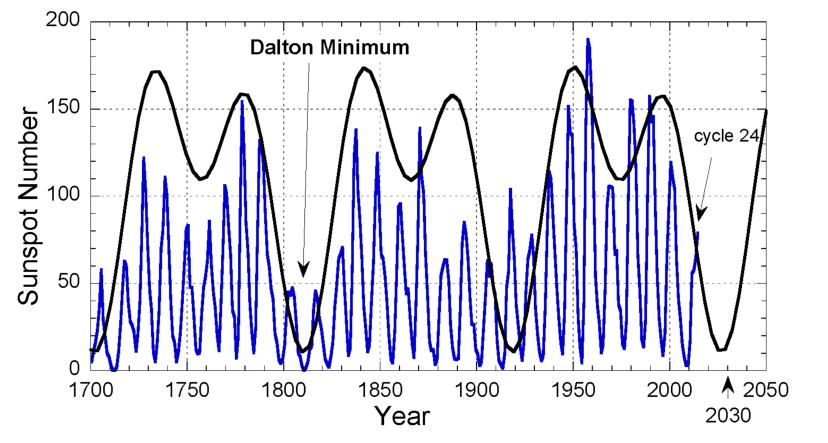
凸函数(Convex Set and Function)
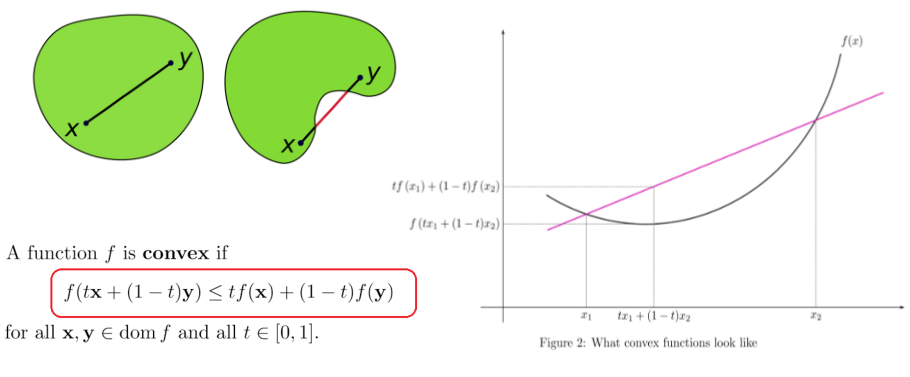
如上图左,t为权重,相当于x,y都属于在0和1之间。
上图右,满足公式的条件就是凸函数。
线性代数(Linear Algebra)
向量(Vector)是一个有方向的标量
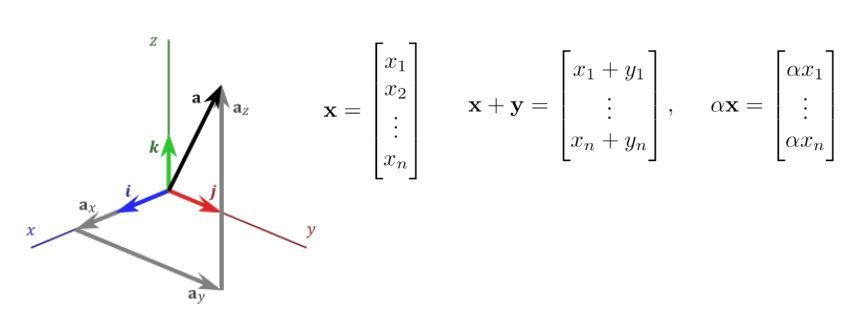
向量空间(vector space)
欧几里德空间(Euclidean space)被数学代表着物理空间和概念,比如,长宽高,角度等。用的笛卡尔坐标系来表示。
$$
\begin{pmatrix} 1 \ 2 \end{pmatrix}
$$
上面是二维向量空间
$$
\left(
\begin{matrix}
1\
2\
3\
\end{matrix}
\right)
$$
上面是三维向量空间
向量的模(Norm of Vectors),向量的范数
$$
\parallel x \parallel
$$
为向量X的范数,
$$
[V;\parallel \cdot \parallel ]
$$
为赋范空间
公理:
$$
\parallel X\parallel \geq 0
$$
$$
\parallel \alpha{X}\parallel = \mid\alpha\mid{\parallel X \parallel}
$$
$$
\parallel X+Y \parallel \leq \parallel X \parallel + \parallel Y \parallel
$$
范数(L-0 TO L-infinity)
链接:范数
- L-0范数
指向量中非0的元素的个数,如果用L0范数来规则化一个参数矩阵W的话,就是希望W的大部分元素都是0,意思就是让参数W是稀疏的。但是实际上我们更多是用是L1范数来实现稀疏,因为L1范数的最有凸近似,而且比L0范数要容易优化求解。总之,L1范数和L0范数都可以实现稀疏,L1因具有比L0更好的优化求解特性而被广泛应用。
例子:
$$
\begin{pmatrix} 1 \ 2\end{pmatrix} \Rightarrow 2 \quad\text{说明非零的个数有两个}
$$
$$
\begin{pmatrix} 1 \ 0\end{pmatrix} \Rightarrow 1
\quad\text{说明非零的个数只有1个}
$$
- L-1范数和L-2范数
L-1norm是两点之间的距离,也称曼哈顿距离(Mahatten Distance),即在欧几里德空间的固定指教坐标系上两点所形成的线段对轴产生的投影的距离总和
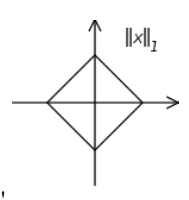
L-2norm是欧几里德距离(Euclidean Distance),也叫欧氏距离,表示在m维空间中两个点之间的距离
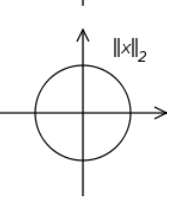
转自:参考链接

在正则化中二者的区别: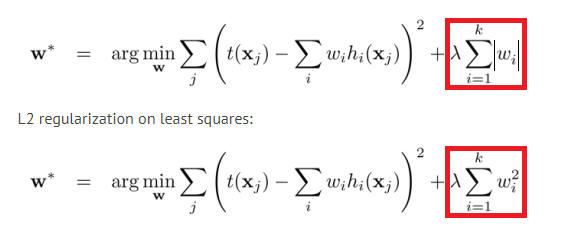
下图是表示曼哈顿距离和欧几里德距离的直观图,曼哈顿距离可能有多解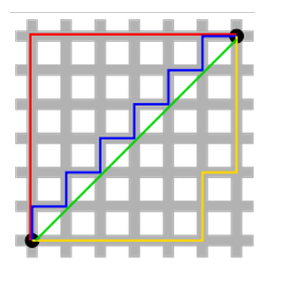
归纳总结:
$$
\parallel x \parallel_p = (\sum_{i = 1}^n {\mid x_i\mid}^p)^\frac{1}{p}
$$
所以当
$$
n = \infty
$$
则公式为
$$
\parallel x \parallel_\infty = (\sum_{i = 1}^n {\mid x_i\mid}^\infty)^\frac{1}{\infty}
$$
$$
\Rightarrow \sqrt[\infty]{\sum_{i=1}^n \mid X_i\mid^{\infty} }
$$
假设存在一个条件:
$$
max(x_1,x_2,x_3,\cdots,x_n) =x_j
$$
$$
x_j\text{里面最大的一个值}
$$
$$
\because x_j^\infty >> x_i^\infty
$$
$$
\parallel x \parallel_\infty = (\sum_{i = 1}^n {\mid x_i\mid}^\infty)^\frac{1}{\infty} \Rightarrow \mid x_j \mid
$$
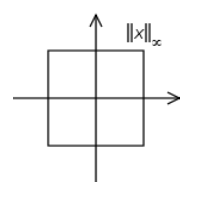
下面是综合的图:
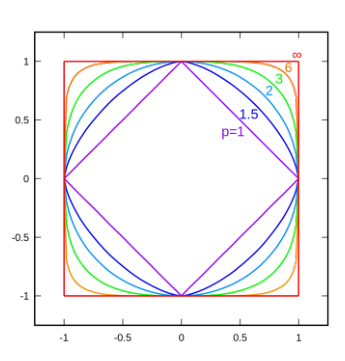
矩阵(Matrix)
向量可以看作是特殊的矩阵,是一个一维矩阵。(dimensions = 1)
欧美的习惯,A表示列矩阵,例如:
$$
A = \begin{bmatrix} a_1 \a_2\a_3\end{bmatrix}
$$
$$
A^T = \begin{bmatrix} a_1& a_2&a_3\end{bmatrix}
$$
$$
\text{说明:}A^T\text{是}A\text{的转置矩阵}
$$

张量(Tensor)
张量这个词最早来自于物理。张量是在标量和向量的基础之上做的进一步推广。
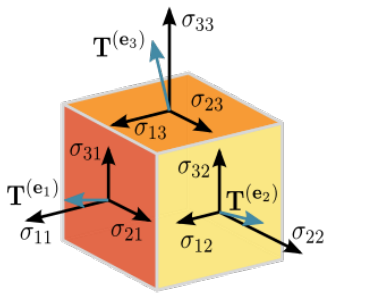
在一个三维的坐标系中,我们可以用三维的向量来表示压力的大小和方向,与此同时我们还需要表示出压力作用的切平面,切平面同样可以用其法向量(垂直于切平面的向量)来表示出来。这种物理量就存在两个方向(力的方向和受力表面的方向),就是一个二阶的张量。实际上标量就是0阶张量,而向量则是一阶张量。
实际上你需要记住的只有一点,在进行张量运算的时候,经常把张量当成多维数组进行计算。
行列式(Determinant)
行列式就是矩阵的值。
表示可以为:
$$
det(A)
$$
$$
detA
$$
$$
\mid A\mid
$$
以上都是行列式的表达方式。
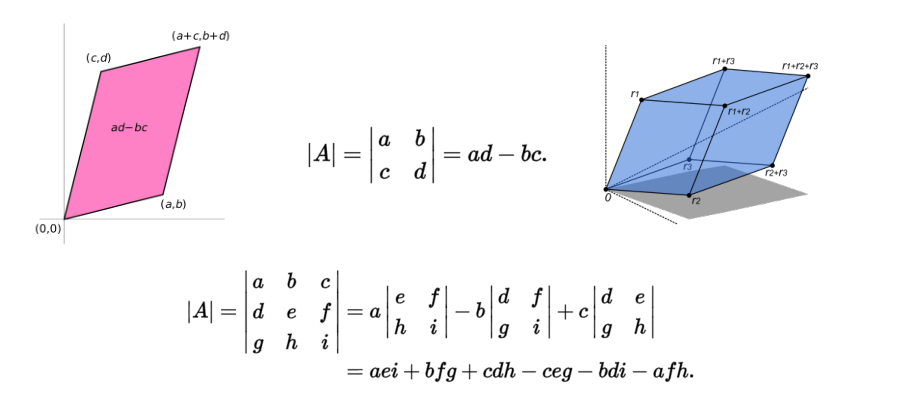
行列式也可以看作矩阵组成的面积。
特征向量(Eigenvector)和特征值(Eigenvalue)
链接:demonstration展示链接
$$
\text{设矩阵A是n阶矩阵,如果数}\lambda\text{和n维非零向量x使关系式}
$$
$$
Ax = \lambda x
$$
$$
\text{成立,那么,这样的数}\lambda\text{成为矩阵A的特征值,非零向量x称为A的对应于特征值}\lambda
\text{的特征向量。}
$$
奇异值分解(SVD:Singular Value Decomposition)
把一个矩阵分成三个矩阵的乘积,其中有一个矩阵是对角矩阵。
如下图: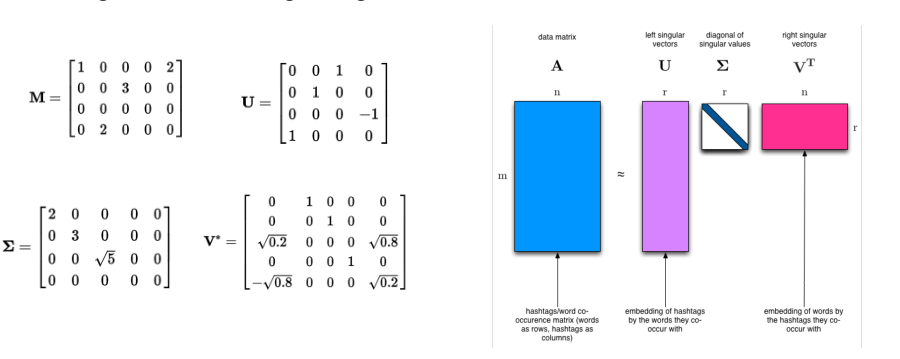
雅可比矩阵和海森矩阵(Jacobian and Hessian Matrices)
在向量分析中,雅可比矩阵是函数的一阶偏导数以一定方式排列成的矩阵,其行列式称为雅可比行列式。
在数学中,海森矩阵(Hessian matrix 或 Hessian)是一个多变量实值函数的二阶偏导数组成的方块矩阵。

参考资料(对于机器学习够用,而且比较全面):
黄博高等数学公式总结:高等数学
黄博的线性代数总结:线性代数


